Essence of Probability Part - 1
Contents

As a kid, I used to play a lot of board games with my cousins. We all would meet on the weekend, sit in the room near the veranda, on the cold marble ground and spend hours playing them. One thing that was common in all the games was dice.
For me, it was fascinating to see how many different games we could play with dice. A dice with just six possible values but can turn the tables at any point in the game. That was my first encounter with the concept called the probability of an event.
Like a board game, all events in our life follow the rules of probability. Some are big events, like weather forecasting. Here we find the probability of kind of weather based on the collected data(previous events). Some events are small and independent of previous events, like tossing a coin to decide who will bat first in a cricket match.
These small and big events are happening billions of times every second, and they decide a lot about what event will happen next. That's what makes this topic so exciting and significant.
This blog is written in shorthand and might not be straight forward to understand. However, If you are already familiar with the concept and are looking to revise. It will help you quickly walk you through the core concepts.
Introduction
One of the fundamental concepts in this subject is Randomness or Uncentertainity. It means something which is not predictable because we lack the sequence of events or data about those events. When you can’t predict the outcome, and there is more than 1 outcome, it’s called a random experiment or trial. All the possible outcomes of a random experiment are called sample space and a subset of a sample space is called an event.
Type of events
- Impossible event: If the event set is empty. I.e $ \varnothing $ or {}
- Sure event: If the event set is equal to sample space. I.e Event Set = Sample Space
- Simple event: If the length of the event set is 1.
- Compound event: If the length of the event set > 1.
Algebra of events
- Complementry event: Let $ A = event $ then $ Not A $ or $ A’ $ exist.
- Union event: $ A \cup B $
- Intersection event: $ A \cap B $
- Event A but not B: $ A - B = A \cup B’ $
Mutually Exclusive Events
- When $ A \cap B = \varnothing $
Exhaustive Events
$$ Let \; S = sample \; space $$ $$ and \; E = Event $$ $$ Then, \quad E_1 + E_2 + … + E_n = S $$
Axiomatic Approach to Probability
$$ P(E) = \frac{number \; of \; outcomes \; of \; E}{ Total \; possible \; outcomes } $$
- For any event $E$, $ \quad 1 \ge P(E) \ge 0 $
- $ P(S) = 1 \quad and \quad P(\varnothing) = 0 $
- If $E$ and $F$ are mutually exclusive. then $ P(E \cup F) = P(E) + P(F) $
$$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$
Conditional Probability
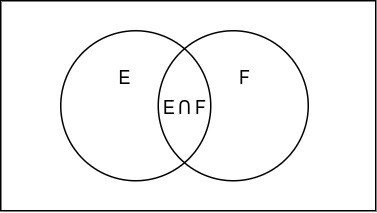
Probability of E given F has occured. It’s denoted by $P(E|F)$
$$ P(E|F) = \frac{P(E \cap F)}{P(F)} = \frac{Number \; of \; outcomes \; for \; E \cap F}{Number \; of \; outcomes \; for F} $$
Properties of Conditional Probability
- $ P(S | F) = P(F|F) = 1$
- $ P( \frac{(A \cup B)}{F}) = P(A|F) + P(B|F) - P(\frac{(A \cap B)}{F}) $ If $A$ & $B$ are mutually exclusive, then $ = P(A|F) + P(B|F)$
- $P(E’|F) = 1 - P(E|F)$
Multiplication Theorm on Probability
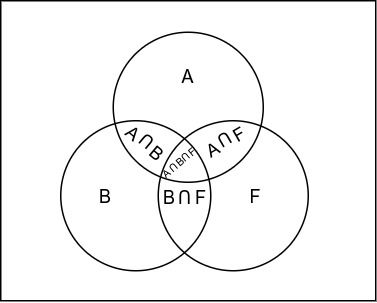
$ P( A \cap B \cap F) = P(A)P(B|A)P(F|A \cap B) = P(A)P(B|A)P(F|AB) $
Independent Events
If $ P(F|E) = P(F) $ and $ P(E) \neq 0 $, then $F$ is an Independent Event.